testing whether a coin is fair
2022-03-06 · 6 min read
Source: https://www.wikiwand.com/en/Checking_whether_a_coin_is_fair
- good problem for applying principles of statistical inference
- good problem for comparing different methods of statistical inference.
for inference, the key questions
- how many trials should we take?
- given some # of trials, how accurate is our estimate of
Pr[H]?
more rigorously, the problem is about determining the parameters of a Bernoulli process given only a limited # of trials.
this article covers two methods (of many):
Posterior PDF (Bayesian approach)
init: true p_H unknown. uncertainty represented by prior distribution. posterior distribution obtained by combining prior and likelihood function (represents information obtained throught the experiment).
p_fair can be obtained by integrating the PDF of the posterior over the "fair" masses?
Bayesian approach is biased by prior (which could be good if it's accurate).
Estimator of true probability (Frequentist approach)
assumes experimenter can toss the coin however many times they wish. first, you decide on a desired level of confidence and tolerable margin of error, which give you the minimum number of tosses needed to perform the experiment.
Posterior PDF #
TODO
Estimator of true probability #
This method depends on two paramters:
- ($Z$) the confidence level, given by a Z-value of the standard normal distribution. Recall that $Z = \frac{\mu_x - \mu}{\sigma_{\mu_x}}$, i.e., deviation of the sample mean $\mu_x$ from the population mean $\mu$, divided by the standard error of the mean $\sigma_{\mu_x}$. Intuitively, if the sample mean deviates by exactly "one sigma", the Z-value is then 1.0.
- ($E$) the maximum acceptable error
Some example $Z$-values:
| $Z$-value | Confidence level | Comment |
|---|---|---|
| 0.6745 | 50.000% | |
| 1.0000 | 68.269% | $\sigma$ |
| 1.9599 | 95.000% | |
| 3.2905 | 99.900% | "three nines" |
| 4.0000 | 99.993% | $4 \cdot \sigma$ |
| 4.4172 | 99.999% | "five nines" |
Let $r$ be the actual probability of obtaining heads. Let $p$ be the estimated probability of obtaining heads.
Here, we just use the MLE for $p$, i.e., $p = \frac{h}{h + t}$ with naximum margin of error $E > |p - r|$.
Recall, the standard error, $s_p$, for the estimate $p$ is: $$ s_p = \sqrt{\frac{p \cdot (1-p)}{n}} $$
The maximum error is given by $E = Z \cdot s_p$, but we can simplify this with an approximation:
Notice that $s_p$ is greatest when $p = (1 - p) = 0.5$. It follows then that $s_p \le \sqrt{\frac{0.5 \cdot 0.5}{n}} = \frac{1}{2 \sqrt{n}}$. Consequently, $E \le \frac{Z}{2 \sqrt{n}}$.
The maximum required number of trials $n$ then follows:
$$ n \le \frac{Z^2}{4 \cdot E^2} $$
Examples #
| $E$ | $Z$ | $n$ |
|---|---|---|
| 0.1 | 1.0 | 25 |
| 0.1 | 2.0 | 100 |
| 0.1 | 3.0 | 225 |
| 0.1 | 4.0 | 400 |
| 0.1 | 5.0 | 625 |
| 0.01 | 1.0 | 2500 |
| 0.01 | 2.0 | 10000 |
| 0.01 | 3.0 | 22500 |
| 0.01 | 4.0 | 40000 |
| 0.01 | 5.0 | 62500 |
| 0.001 | 1.0 | 2.50e5 |
| 0.001 | 2.0 | 1.00e6 |
| 0.001 | 3.0 | 2.25e6 |
| 0.001 | 4.0 | 4.00e6 |
| 0.001 | 5.0 | 6.25e6 |
General Case #
Consider the distribution of the sample mean, $\mu_x$, (assuming we took many samples with $n$ trials each). Note the population mean $\mu$ and the standard error of the mean, $\sigma_{\mu_x}$ (the stddev of the sample mean).
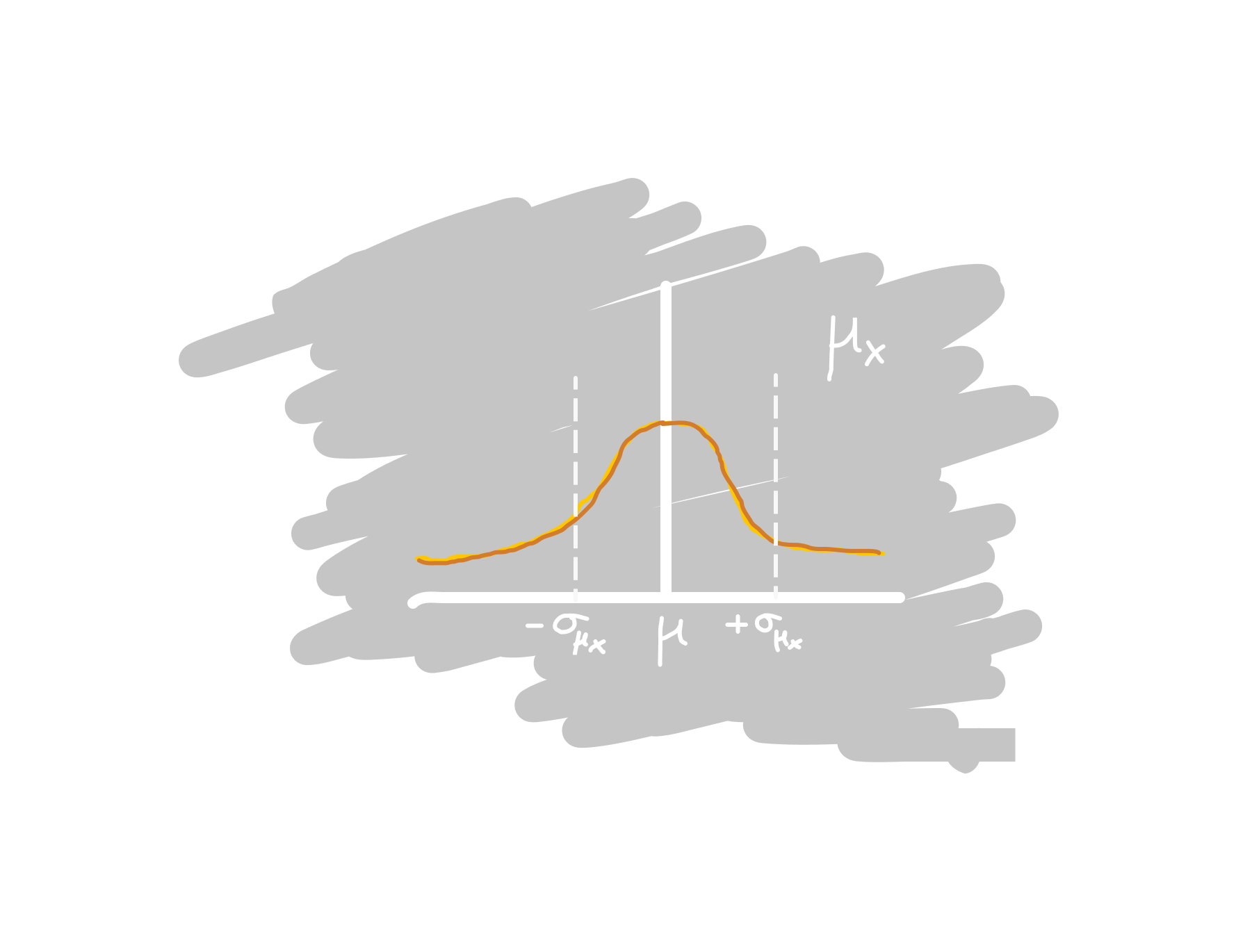
One interesting question is: given a fixed number of trials, say $n = 1000$, what should our maximum tolerated absolute deviation, $E$, be? What is our key parameter for choosing a good $E$?
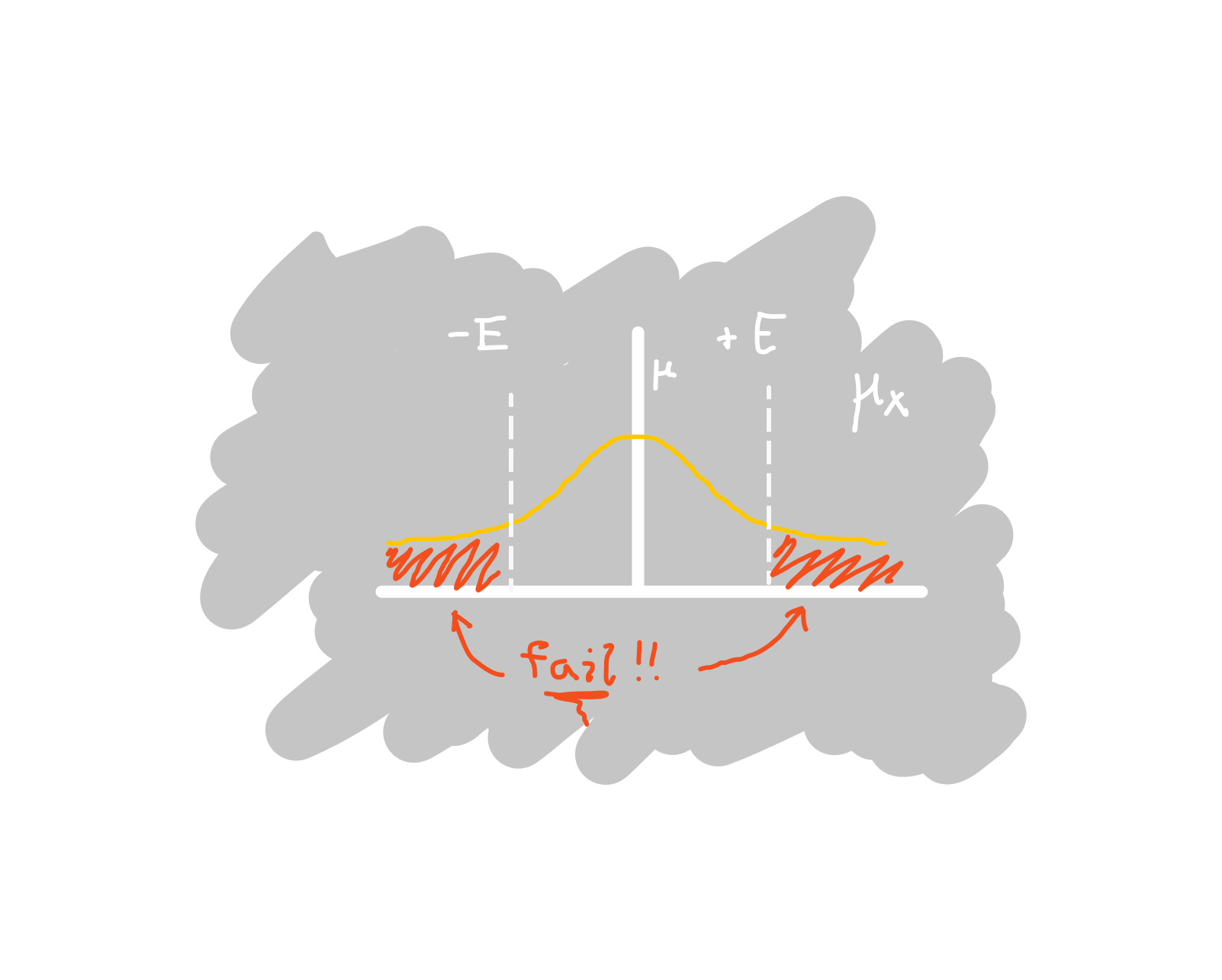
We should choose $E$ based on our required confidence. Given that the samples are actually drawn from the population, we want some small probability of failure (or inversely, a large probability of success), where our statistical criterion decides that the samples are not actually drawn from the population.
Using the maximum absolute deviation $E$ as a criterion, we will claim the two distributions are not the same if the sample mean $\mu_x$ lies within the red "fail" zone above.
More precisely, our failure probability is the probability that $\mu_x$ is outside of the interval $[\mu - E, \mu + E]$:
$$ Pr[failure] = Pr[(\mu_x < \mu - E) \cup (\mu + E < \mu_x)] $$
Since the sample mean is normal (law of large numbers), the upper and lower probabilities are identical, so we can simplify as
$$ Pr[failure] = 2 \cdot Pr[\mu_x < \mu - E] = 2 \cdot F_\mu(\mu - E) $$
where $F_\mu$ is the CDF of the normal distribution $N(\mu, \sigma_{\mu_x})$. By normalizing the interval bounds in terms of the standard normal distribution, we can see
$$ Pr[failure] = 2 \cdot \Phi\left(\frac{(\mu - E) - \mu}{\sigma_{\mu_x}} \right) = 2 \cdot \Phi\left(\frac{-E}{\sigma_{\mu_x}} \right) $$
where $\Phi$ is the CDF of the standard normal distribution. Given a desired $p_f = Pr[failure]$, we can compute the error bounds $E$
$$ \begin{align*} p_f &= 2 \cdot \Phi\left(\frac{-E}{\sigma_{\mu_x}} \right) \ \frac{-E}{\sigma_{\mu_x}} &= \Phi^{-1}(p_f / 2) \ E &= -\sigma_{\mu_x} \cdot \Phi^{-1}(p_f / 2) \ \end{align*} $$
Of course, it can be annoying to compute the inverse normal CDF, so it's often useful to frame $p_f$ in terms of the Z-score, or "standard sigma's from the mean (0)". There's a convenient table above, showing the Z-value alongside the $1-p_f$ success probability for a few values.
For example, if our standard error of the mean is $\sigma_{\mu_x} = 50$ and our desired confidence is $\sigma_{std} = 5.0$, then our error bound is $E = \sigma_{\mu_x} \cdot \sigma_{std} = 250$.
If we take more samples, our SME might only be $\sigma_{\mu_x} = 15$. For the same confidence, our required error bounds would only be $E = 75$.
Likewise, if we decrease our desired confidence to only $\sigma_{std} = 1.5$ while our $\sigma_{\mu_x} = 50$, the required error bounds are also $E = 75$.
Intuitions #
- Take more samples to allow tighter error tolerance or allow lower required confidence (for the same failure probabilty).
- Using a very high required confidence can make your absolute error bound very large, which might mean you are not really saying much about the sample distribution.